Machine Learning : classification à l'aide des arbres de décisions : fonctionnement et application en NodeJS

Qu’est ce qu’un arbre de décisions

Un arbre de décision est une représentation visuelle d’un algorithme de classification de données suivant différents critères qu’on appellera décisions (ou noeuds). Voici un exemple :

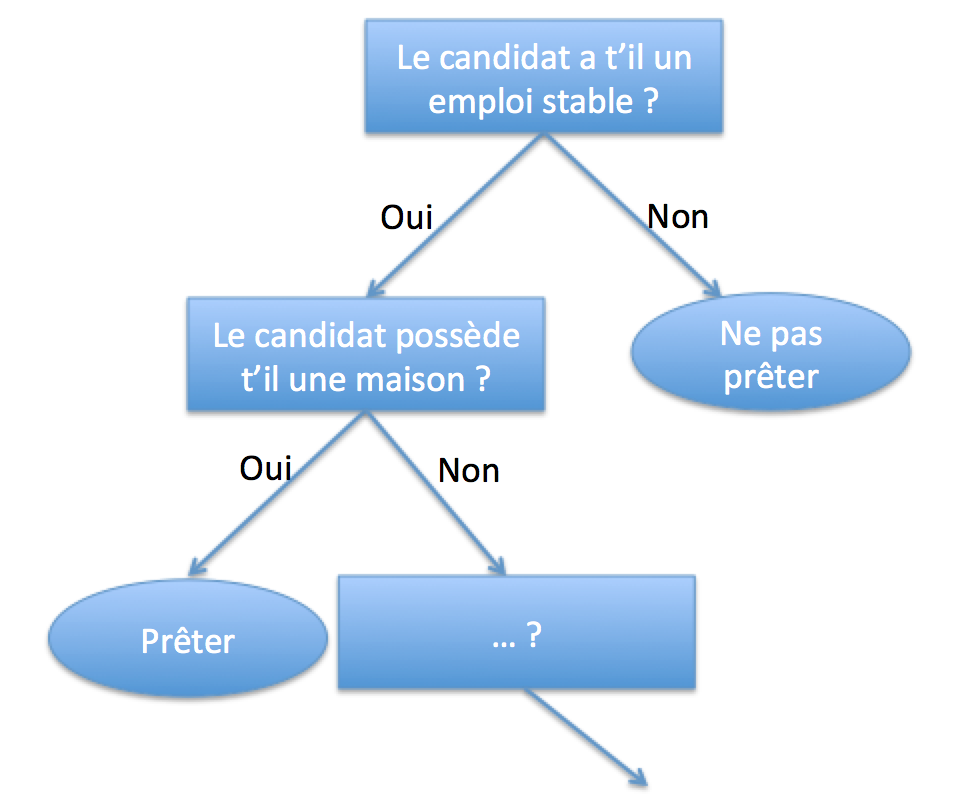
Cet arbre de décision permet en fonction de quelques questions de déterminer si une banque doit prêter ou pas au client qui demande un prêt. Ce dernier est très simplifié mais la plupart des banques utilisent des systèmes similaires permettant aux agents une prise de décision experte.

Mais comment arrive t’on à de telles règles de décisions. Dans les faits il s’agit de synthétiser la connaissance et l’historique de l’ensemble des prêts accordés par la banque et de classer chacun de ces prêts selon qu’ils aient été remboursés sans incident ou pas. Il s’agit donc de trouver dans une énorme quantité de données les questions qu’il est judicieux de poser afin de prédire la qualité d’un emprunteur.

Vocabulaire

Nous allons détailler la construction d’un tel arbre de décision. Posons d’abord quelques mots de vocabulaire. On va classer des objets.

• Chaque objet de la données historique (set d’entraînement) dispose d’une classe bien définie
• Chaque objet (par exemple un prêt accordé à monsieur X) dispose de features, de propriétés bien définies elles aussi. Par exemple : la personne a qui on a accordé le prêt possédait-elle une maison, possédait elle un CDI ?
• Chaque propriété ou feature a un ensemble de valeurs possibles. Par exemple (‘oui’ ou ‘non’)

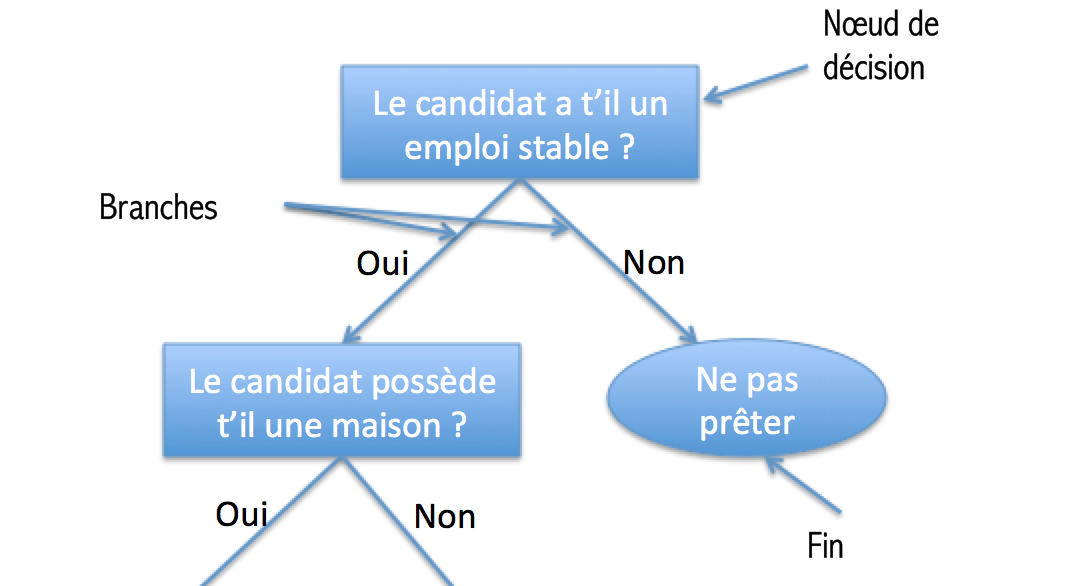
Dans notre graphique représentant l’arbre de décision on a les éléments suivants :

• Un noeud de décision (représenté par un rectangle) (on pose une question)
• Un bloc de fin qui est représenté par un oval. (on a trouvé la classe)

Fonctionnement de l’algorithme : un exemple

Dans les faits on aura en entrée de notre algorithme une série de données qui représentera de nombreux objets (ici des prêts) ayant chacun un set de propriétés (ici : CDI oui ou Non, Locataire oui ou non …). Ces objets du set d’entrainement seront déjà classés (ex: Bon Emprunteur).Par exemple :

Prêt 1 : CDI : 1 - Locataire : 1 - Classe : Bon emprunteur
Prêt 2 : CDI : 0 - Locataire : 0 - Classe : Bon emprunteur
Prêt 3 : CDI : 1 - Locataire : 1 - Classe : Bon emprunteur
Prêt 4 : CDI : 0 - Locataire : 0 - Classe : Mauvais emprunteur
Prêt 5 : CDI : 1 - Locataire : 1 - Classe : Bon emprunteur
...

Notre algorithme va donc devoir choisir une première question à poser à notre candidat. Pour cela il doit choisir la feature (ou propriété) qui permet de découper nos prêts en deux sets les plus homogènes possibles, c’est à dire deux sets regroupant des prêts dont les emprunteurs sont en grande partie d’une même catégorie.

Par exemple l’algorithme va tester la feature CDI et va ensuite répartir les prêts dans deux set : les prêts fait par des personnes en CDI et les autres. Si dans un des set on trouve que des prêts ayant la même classe alors l’algorithme s’arrêtera pour cette branche. Par exemple si on constate que tous les gens qui n’ont pas de CDI sont des mauvais emprunteurs alors on peut s’arrêter là et dire à nos agents de ne plus prêter aux gens sans CDI.

Si on a pas obtenu un set composé de prêts qui ont la même classe après ce premier split, on va ensuite refaire le même travail pour les features suivantes. Nous allons sélectionner la feature permettant un classement le plus homogène possible… Ce processus est mené jusqu’à ce qu’o obtiennent des classes homogènes.

Overfitting et extraction de sens

Cet algorithme est peu gourmand en mémoire. Mais il y a un risque très important d’overfitting, c’est à dire que l’arbre n’est pas utilisable car il fournit des résultats très bon pour le set d’entraînement, mais utilisé en conditions réelles il classe très mal les nouveaux exemples. Pour cela on peut envisager d’avoir couper notre set d’entrainement en deux afin d’avoir un set de données permettant de valider si il y a overfitting ou pas.

Cet algorithme est très intéressant pour extraire de l’information d’une source de données obscure. Il permet d’isoler les propriétés ou features qui apportent le plus d’information pour déterminer la classe de chaque objet.

Application en NodeJS

Calcul de l’entropie de Shannon

Dans le paragraphe précédent nous disions qu’il fallait trouver la feature générant des classes qui sont les plus homogènes possibles. Mais comment définir cette homogénéité ?

Nous allons utiliser un résultat important de la théorie mathématique de l’information : l’entropie. Et plus particulièrement l’entropie de Shannon :

$H=-\sum_{i=1}^{n} P(x_{i})log_{2}(P(x_{i}) )$

L’entropie correspond au désordre. Plus on a de classes différentes dans un set de données plus l’entropie sera grande. De manière opposée si dans un set de données tous les objets ont la même classe, il n’y aura pas de désordre l’entropie sera nulle.

Dans les faits on va calculer l’entropie de la manière suivante en NodeJS :

var _ = require('lodash');
/**
* This function is used to compute the Shannon Entropy
* @method calculate_shannon_entropy
* @param  {Array}                  data an array of data
* @return {Number}                       The Shannon Entropy
*/
var calculate_shannon_entropy=function(data){

  // init the shannon Entropy
  var shannon_entropy = 0;
  // we get the number of entries in the array
  var length_of_data = data.length;
  // create an empty array to keep track of different labels
  var labels_counter = {}
  // we iterate through the array
  _.forEach(data, function(value, key) {
    // extract the label from the one data element
    var label_extracted = value.label;
    // check if this label is inside our label counter array
    if (label_extracted in labels_counter){
      // the element is inside our object increment its value
      labels_counter[label_extracted] +=1
    } else {
      labels_counter[label_extracted] = 1
    }
  });

  // We then iterate through our label counter object
  _.forEach(labels_counter, function(value, key) {
    // we get the frequency of the number of time a label occurs
    var p = parseFloat(value/length_of_data)
    // Caculate the entropy of a class and add it to the shannon_entropy variable
    shannon_entropy -= p * getBaseLog(2,p)

  })

  return shannon_entropy

}

/**
* This function return the log of Y in base X
* @method getBaseLog
* @param  {Number}   x base
* @param  {Number}   y number
* @return {Number}     the log of Y in base X
*/
var getBaseLog=function(x, y) {
  return Math.log(y) / Math.log(x);
}

var a = [
  {"has_a_car":1, "has_a_house":1, "has_children":1,"label":"bon_emprunteur"},
  {"has_a_car":1, "has_a_house":1, "has_children":0,"label":"bon_emprunteur"},
  {"has_a_car":1, "has_a_house":0, "has_children":1,"label":"bon_emprunteur"},
  {"has_a_car":0, "has_a_house":0, "has_children":0,"label":"mauvais_emprunteur"},
  {"has_a_car":0, "has_a_house":0, "has_children":1,"label":"mauvais_emprunteur"}
]
calculate_shannon_entropy(a)
// returns 0.9709505944546686

On prend donc la fréquence d’apparition de la classe bon_emprunteur et son log en base 2 auquel on va ajouter moins la fréquence d’apparition de la classe mauvais_emprunteur et son log en base 2 !

Il va falloir ensuite que l’on puisse éliminer des features au fur et à mesure que l’on split notre données au fil des blocs de décision. C’est l’objet de la partie suivante :

Création de la fonction permettant de partitionner un set de données en fonction d’une feature et de sa valeur

Notre mission ensuite est de préparer la fonction qui permet à partir d’un set de données d’entrainement de récupérer un set plus petit ne contenant plus que les objets disposant de cette feature dont la valeur est égale à une des valeurs possibles de la feature.

/**
* This function split our dataset and extract object that have the feature set to a specific value
* @method split_the_dataset_by_feature_and_value
* @param  {Array of Object}                               data    our dataset
* @param  {String}                               feature the name of the feature
* @param  {String or Number}                               value   the value of the feature to extract from the dataset
* @return  {Array of Object}                               value   the dataset without the objects that have the feature "feature" set to the value "value" & without the feature "feature"
*/
var split_the_dataset_by_feature_and_value=function(data_set,feature,value){
  // we partition our array in order to isolate in the data
  // Objects that have the `feature` set to the right value
  var data_set


  var array_partitioned = _.filter(data_set, function(o) { return o[feature]==value; });
  // we then have to remove the feature from our objects
  var array_to_return = []


  array_partitioned.forEach(function(v){
    var new_object = {}
    _.forEach(v, function(value, key) {

        if(key!==feature){
          new_object[key]=value
        }
      });
    array_to_return.push(new_object)

  });

  return array_to_return
}

split_the_dataset_by_feature_and_value(a,"has_a_house",0)
// returns
// [ { has_a_car: 1, has_children: 1, label: 'bon_emprunteur' },
//  { has_a_car: 0, has_children: 0, label: 'mauvais_emprunteur' },
//  { has_a_car: 0, has_children: 1, label: 'mauvais_emprunteur' } ]

Par exemple ici nous nous débarassons des objets dans notre set de données dont la feature has_a_house est différent de 0.

Maintenant attaquons nous au coeur du réacteur : nous devons trouver la meilleur feature, autrement dit celle qui génère le moins d’entropie (on parle aussi de gain informationnel maximal)…

Déterminer la feature dans un set de données générant un gain informationnel maximal

var _ = require('lodash');
var data_set_splitter = require('./data_set_splitter')
var shannon_entropy = require('./shannon_entropy')

/**
* This function will select the best feature for splittingwith the help
* of the shannon entropy
* @method get_the_best_feature_for_splitting
* @param  {Array}                           data  A dataset of training, an array conposed of object with a property "label" that represents the class
* @return {String}                                The name of the best feature for splitting (the property name)
*/
var  get_the_best_feature_for_splitting= function(data){
  // we compute the Entropy
  var base_entropy_value = shannon_entropy.calculate_shannon_entropy(data)
  // init a variable that will contain the best informational gain value
  var best_informational_gain_value = 0
  // init a variable that will contain the best feature choice for splitting
  var best_feature_name = ""
  // we iterate through our features (we take the first data element)
  _.forEach(data[0], function(value_of_feature, feature_name) {
    if(feature_name != "label"){


      // get the unique values of each feature
      var unique_values_of_this_feature = _.uniq(_.map(data, feature_name));
      // init a variable that will contain the new_entropy_value
      var new_entropy_value = 0;
      // iterate through each possible value of this feature
      _.forEach(unique_values_of_this_feature, function(value_of_this_feature, key) {

        var  data_set_without_this_feature_of_value = data_set_splitter.split_the_dataset_by_feature_and_value(data,feature_name,value_of_this_feature)

        var p = parseFloat(data_set_without_this_feature_of_value.length/data.length)
        new_entropy_value += p*shannon_entropy.calculate_shannon_entropy(data_set_without_this_feature_of_value)

      })

      // we can now have the informational gain for this specific feature
      var informational_gain_value = base_entropy_value - new_entropy_value
      // if the informational gain value is higher than the best one
      if(informational_gain_value > best_informational_gain_value){
        // it now become the best informational gain
        best_informational_gain_value = informational_gain_value
        // and the best feature has to be keep in memory
        best_feature_name = feature_name
      }
    }

  });
  return best_feature_name;
}

get_the_best_feature_for_splitting(a)
// returns "has_a_car"

module.exports = {
  get_the_best_feature_for_splitting:get_the_best_feature_for_splitting
}

Cette fonction doit détecter quelle est la feature qui apporte un gain informationnel maximal. Nous cherchons en effet à trouver la feature permettant de diviser nos exemples dans des “compartiments”, “compartiments” qui doivent avoir la particularité de regrouper des exemples de classes similaires, et ce dans une proportion la plus importante possible. Ainsi nous réduisons le désordre.

Dans les faits nous allons faire usage du calcul de l’entropie de Shannon pour calculer cette notion de différentiel de désordre.
Si on prend l’exemple de la feature has_a_car, on a donc deux valeurs possibles : vrai ou faux. Première étape : l’algorithme va donc générer un set de données ne contenant pas les exemples dont la has_a_car vaut vrai. On calcule ensuite le rapport entre le nombre d’éléments de notre nouveau set de données et le nombre d’élément que contient le set de données d’origine. On calcule ensuite l’entropie avec ce nouveau jeu de données. Ce processus est répété pour chaque valeur de la feature (donc 2 fois ici). On calcule ensuite pour chacune des feature le gain informationnel.

Ce dernier étant défini comme la différence entre l’entropie de base et la somme des entropies (pour chaque valeur de la feature). L’algorithme sélectionnera la feature qui permet d’obtenir le meilleur gain informationnel !

Construction de l’arbre de décisions de manière récursive

Il est temps de construire notre arbre. Nous allons le faire grâce à l’usage d’une fonction récursive, c’est à dire une fonction qui va elle même s’appeler au cours de son exécution. Pour plus d’informations sur la récursivité rendez-vous sur la page wikipédia : https://fr.wikipedia.org/wiki/Fonction_r%C3%A9cursive.

Lorsqu’on bâtit une fonction récursive il faut en premier lieu visualiser nos conditions de sorties. Nous allons donc itérer sur notre jeu de données d’entrainement afin à chaque fois de détecter la meilleur feature permettant de diviser notre jeu de données. Ainsi à chaque itération on isole la meilleure feature, on débarasse notre jeu de données de cette dernière. Cette meilleure feature sera donc une feuille de notre arbre. De cette feuille on aura autant de ramifications que de valeurs possibles à cette feature. Chaque feuille sera ensuite générée de suivant le même algorithme. Les conditions de sorties seront donc au nombre de deux :

• Il ne reste plus de features dans le jeu de données
• Il ne reste plus que des objets ayant tous la même classe.

Voici l’algorithme :

var _ = require('lodash');
var data_set_splitter = require('./data_set_splitter')
var best_feature_selector = require('./best_feature_selector')
var shannon_entropy = require('./shannon_entropy')

/**
 * This method will generate a decision tree
 * @method generate_decision_tree
 * @param  {Array of object}               data The dataset
 * @return {Object}                    The decision tree/ ex : {"has_a_car":{"yes":{"has_a_house":{"yes":"good_borrower","no":"bad_borrower"}},"no":"bad_borrower"}}
 */
var generate_decision_tree = function(data){

  // Because we build a recursive function
  // we have to set our stopping conditions at the
  // top.

  // group the dataset by label
  var grouped_data_per_label = _.groupBy(data, function(o){
    return o.label
  });

  // We stop when there are only elements of the same class
  // inside the dataset
  //
  if(_.size(grouped_data_per_label)===1){
    return Object.keys(grouped_data_per_label)[0]
  }



  //  If there is no more features to split
  //  The size of the first training is only 1 because
  //  there is just one property the class
  //  ex : data[0] = {"label":"good_borrower"}
  if(_.size(data[0])===1){
    return mostly_present_class(data)
  }




  // Get the best feature to split
  var best_feature_for_splitting = best_feature_selector.get_the_best_feature_for_splitting(data)

  // create the object decision tree
  var decision_tree ={}
  decision_tree[best_feature_for_splitting]={}

  // we have then to extract the unique values of this feature in the dataset
  // get unique values of this feature
  var unique_values_of_best_feature =  _.uniq(_.map(data, best_feature_for_splitting));
  // forEach unique values of this feature
  _.map(unique_values_of_best_feature, function(value_of_this_feature) {


    // We get the dataset cleaned of examples that have a feature "best_feature_for_splitting"
    // set to the value : "value_of_this_feature"
    var new_data_set = data_set_splitter.split_the_dataset_by_feature_and_value(data,best_feature_for_splitting,value_of_this_feature)
    decision_tree[best_feature_for_splitting][value_of_this_feature] = generate_decision_tree(new_data_set);

  });


  return decision_tree

}


module.exports={
  generate_decision_tree : generate_decision_tree
}

On obtient donc le résultat suivant pour notre set de données d’exemple :

{"has_a_car":{"yes":{"has_a_house":{"yes":"good_borrower","no":"bad_borrower"}},"no":"bad_borrower"}}

L’ensemble du code se trouve sur mon repo github : https://github.com/maximilienandile/decision_tree_example